2018-03-20

BigQuery の standard sql にも ROLLUP はあるよ

背景

上手いこと使うと、全体の合計と、group で指定したそれぞれの合計が同時に取得できる rollup だが、日本語のBQの標準SQLのページには記載がない(2018/03/20現在)

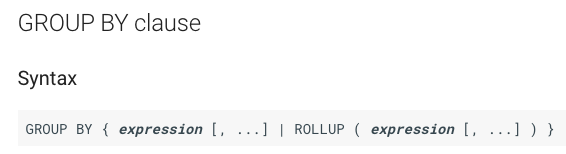
具体的には次のような感じ

解決法

次のように言語の設定を英語にしよう。

すると group by の説明に…

2018-03-12

データ解析のためのロジスティック回帰モデルを少し読んだ

背景

前から欲しかった本がある。Applied Logistic Regression 3rd Edition であるが、ご覧の通り、ハードカバーで1万6千円、Kindle 版でも1万円してしまう。

まず、Logistic Regression（ロジスティック回帰）であるが、深層学習ほど最新の研究成果があるわけでもないが、よく使う。機械学習やビッグデータを扱うデータサイエンティストの年収や使用言語などを赤裸々にするデータ - GIGAZINEによると、Logistic Regressionは最も使われる機械学習手法で、63.5％のデータサイエンティスト（回答者）に使われるとされている。また自分も仕事で使っているし、今後も使うと思われる。

この本のすごいところは1989年に初版が出てから、進化し第三版まで来ているところである。よく、統計や機械学習の質問サイトである、 Cross Validated でも取り上げられている。かなり有名な書籍らしい。でも高い。

ある時ふと twitter のタイムラインを見ると、

おらにはわがんね pic.twitter.com/m1aLHF5iWq
— ミス理科大No.5 鈴木りか (@misstus2017_05) 2018年2月1日

というものが見えた。ぼやけてよく読めないがよくみると、Applied Logistic Regression と書いてあるではないか。それも日本語訳の書籍らしい。データ解析のためのロジスティック回帰モデルという書籍らしい。それも 3rd Edition！調べてみると、なーんと、Amazon で 8856円。それも中古も出ている。早速（中古を）注文した。

内容を少し

確かに難しい。第一章の一節目の一行目から、「応答変数」と「説明変数」がいきなり出て来るが、それについて何も説明がない。そして、すかさず「独立変数（共変数）」が出て来るが、それ自身の説明ではなく、統計の回帰の目的について、である。

おそらく、この節で言いたいのは、ここを読んでわからない人には、この本はおすすめできません、といいたいのだろう。だから、この本は初心者用や勉強用ではなく、実用（プロもしくは学生であればそれを使って研究している人）レベル（英語タイトルは確かにそうなのかも）と思った方がいいだろう。

まとめ

盛り上げといてなんだけど、少なくとも初心者にはおすすめできない。統計などの知識（例えば Wald検定、尤度比検定、Score検定）も必要（一章を読む限り）。自分はとりあえず必要なところだけ読むみたいな仕方をしているが、Webにある他の情報をなどと照らし合わせながら、読んでる…。

2018-01-31

Jupyter notebook (Python3) で mypy のチェックを行う

背景

python3 で導入された型ヒントだが、そのままだと静的にも動的にもアノテーション（単なるコメント）として扱われるらしく、ちょっと残念。 mypy というコマンドで型チェックを行ってくれるらしい。Jupyter notebook 上でも実行したい。

対応

mypy をインストールする。

pip install mypy

typecheck.py をダウンロード

ipython の profile ディレクトリの start up で typecheck.py をダウンロード

cd ~/.ipython/profile_default/startup
curl https://gist.githubusercontent.com/knowsuchagency/f7b2203dd613756a45f816d6809f01a6/raw/c9c1b7ad9fa25a57ee1903d755d5525894ffa411/typecheck.py -o typecheck.py

最新版?は、 A cell magic to enable the use of mypy within jupyter notebooks · GitHub で確認すること

カーネルの再起動

jupyter notebook の再起動でもいいけど、あのリロードボタン。

magics を評価したいセルに埋め込む

次の magics を使いたいセルの先頭に埋め込む

以下は例：

%%typecheck --ignore-missing-imports

foo: int

foo = 'var'

すると、<string>:5: error: Incompatible types in assignment (expression has type "str", variable has type "int") とエラー（警告）が表示される。これが見たかった。

まとめ

あまり jupyter で使っている例を見ないけど、mypy は jupyter notebook で使える。

追記

残念なことに magics はセルごとに起動するので、別のセルの型ヒントや別のセルの typing から import した型は見えてないかもしれない（というか magics の仕組み上恐らく見えていないだろう）。セルごとに毎度 import したり、まとめられるセルはまとめてしまうなどの工夫が必要。

参考

journalpanic.com

2018-01-24

「被害者が犯行可能な人を犯人の候補」とするWald法

背景

二項分布やベルヌーイ試行の確率の信頼区間を求める方法として、Wald法というものがある。非常に気持ち悪いと思うのだが、まだ多くの人がその気持ち悪さを理解していないと思うので、自分の力不足を感じながらも書いた。

Wald 法

正規分布は $n\mu > 5, n\sigma^2 > 5$ のとき、ベルヌーイ試行の確率によい近似となるらしい。ここで、 $\mu, \sigma^2$ はそれぞれ、母平均、母分散、 $n$ は試行回数。

正規分布 $N(\mu, \sigma^{2}/n)$ の信頼区間

$\displaystyle \mu \pm z\sqrt{\sigma^{2}/n}$

である。ここで、 $z$ は正規分布分位数。ベルヌーイ試行の成功確率の分散は $\mu(1-\mu)$ と平均を使って表すことができるので、正規分布で近似したベルヌーイ試行の母平均の信頼区間は

$\displaystyle \mu \pm z\sqrt{\mu(1-\mu)/n}$

となる（一つ目の近似。分布の近似）。

さらに 試行回数が多くなれば 中心極限定理により、標本平均は母平均に近づく。

よって母平均を標本平均と標本分散に置き換える（二つ目の近似。今度は値の近似）。すなわち、 $m$ を標本平均とする。よって、母平均を標本平均と近似し、さらに分布も正規分布で近似した、ベルヌーイ試行の成功確率の母平均の信頼区間は $\displaystyle m \pm z\sqrt{m(1-m)/n}$

となる。これが Wald 法。

Wilson score interval

母平均が分かっていたなら、標本平均はどのように分布するだろうか。標本平均の分布は、正規分布 $N(\mu, \sigma^{2}/n)$ に従うと仮定すると、確信区間 *1

$\displaystyle \mu \pm z\sqrt{\mu(1-\mu)/n}$

に入ることになる（一度目の近似）。

ある母平均 $\mu$ を考えたとき、観測された標本平均 $m$ がこの確信区間の外だったとき、その母平均 $\mu$ は信頼区間の外であると考える。

これが、Wilson score interval の考えである。

続けると、この信頼区間の境界は次のようにして求める。

次の式を満たすとき、標本平均 $m$ は確信区間に入っている。

$\displaystyle |\mu - m| \le z \sqrt{\mu(1-\mu)/n}$

両辺二乗して、

$\displaystyle (\mu - m)^2 \le z^2 \mu(1-\mu)/n$

が得られる。ところで、区間の境界は等号が成り立つところである。すなわち、

$\displaystyle (\mu - m)^2 = z^2 \mu(1-\mu)/n$

である。これは $\mu$ についての二次方程式なので、それを解くと、

$\displaystyle \mu = \frac{m+t/2 \pm \sqrt{ m(1-m)t + t^2/4} }{ 1+t }$

ここで、 $t=z^2/n$ (論文の式)

これが Wilson score interval である。

考察

Wilson score interval を考えると Wald 法の気持ち悪さが浮き出てくる。

母平均の信頼区間を求めるのに、母平均を標本平均で近似している。

犯人を推定するのに、被害者を一旦犯人とおいて、被害者が犯行可能な人を本当の犯人の候補とするのがWald法である。

それでうまくいことがあるとしても気持ち悪すぎる。

参考

http://www.barestatistics.nl/uploads/1/1/7/9/11797954/wilson_1927.pdf

*1:信頼区間と区別するために敢えてこのように書く

2018-01-24

mac が重くてたまに熱か何かで落ちたのでその時のメモ

背景

mac が重くてたまに熱か何かで落ちる。vagrant で動いているものがあるので、それが原因かと思ったが、 top で確認すると、mds_stores というプロセスが動いていた。

対応

下記のページを参考にしようとした。

blog.tottokug.com

ところが、

sudo locate .git

で気がついたが、locate が動いていない。普通は locate を使うので、エラーメッセージに従い、下記のコマンドを実行

sudo launchctl load -w /System/Library/LaunchDaemons/com.apple.locate.plist

そして、locate あれば、spotlight は使わないので、spotlight を停止することに。

qiita.com

を参考に、

 sudo mdutil -a -i off

これで止まった。（はず）

念のため、top コマンドで確認すると、mds_stores　は消えたものの、 mdworker というのが数個生きているみたい。

qiita.com

を参考に、

sudo launchctl unload -w /System/Library/LaunchDaemons/com.apple.metadata.mds.plist

を実行。確認すると消えていた。

2018-01-19

正規分布の分位点関数（パーセント点関数）の近似

背景

正規分布の分位点（パーセント点）は数値計算ライブラリの分位点関数を使えば簡単に求められる。例えば、python だと、scipy.stats.norm の、ppt だ。ところが、SQL には標準でないようである。自分で関数を作ってもいいが、ここはSQLでかける近似式をつかってもいいかもしれない。

近似式を調べる

いろいろ調べたが、Hastings 1955 は有名だが、その後多くの近似式があるようである。全部を調べるは大変で、サーベイっぽい論文などもあるのだが、最終的には、多く場合分けをして、多く次数を増やしていけば、近似精度がよくなるという話。これはドメイン依存で、すなわち、どのような状況でどの程度近似精度が重要なのかと、SQLなどで記述する場合に複雑になっていってもいいのかというトレードオフの問題がある。あと、近似式だから、正解はなく、多くの大量に考え出されているので、それら全てを評価するのもコストがかかる。

というわけで、私が探した中で、一番シンプルな式の山内 1965から検証する。

正規分布の分位点関数の近似式山内 1965

戸田英雄, 小野令美「正規分布のパーセント点を求めるミニマックス近似」(1993) によると式は

$\begin{align} \left[ y \left( 2.0611786 - \frac{5.7262204}{y + 11.640595} \right) \right] ^{ \frac{1}{2} }, \\ y = - \log 4P(1-P) \end{align}$

らしい。 $y$ の部分がまとめられてしまっているが係数も3つで乗数もなく、入力の間違いの確認も容易である。二乗根と対数ならSQLもサポートしている。

python での近似性能の検証

多くの場合分位点そのものに興味はない。だから分位の近似の評価ではなく、近似された分位点から逆に計算された分位*1が元の分位と比べてどうだったかを調べる。

import numpy as np

def yamauchi1965(q):
    y = -np.log(4*q*(1-q))
    return np.sqrt(y*(2.0611786-5.7262204/(y+11.640595)))

def yamauchi1965_sql(q):
    return np.sqrt(-np.log(4*q*(1-q))*(2.0611786-5.7262204/(-np.log(4*q*(1-q))+11.640595)))
    # sqrt(-log(4*Q*(1-Q))*(2.0611786-5.7262204/(log(4*Q*(1-Q))+11.640595)))

# 検証用
from scipy.stats import norm
for i in [1, 10, 20, 50, 100, 1000, 10000, 100000]:
    q = 1.0-1.0/2/i
    z = norm.ppf(q)
    z1 = yamauchi1965(q) # これが近似の分位点z1
    q1 = norm.cdf(z1)    # 近似の分位点z1から、元の分位を逆計算q1
    r = 1-(1-q1)/(1-q)   # 分位(1-q)と近似から逆計算した分位(1-q1)の割合の違い（割合）からさらに１を引いて相対的な差を求める
    print("q: %f, z: %f, z1: %f, q1: %f, r: %f" % (q, z, z1, q1, r))

実行結果

q: 0.500000, z: 0.000000, z1: -0.000000, q1: 0.500000, r: 0.000000
q: 0.950000, z: 1.644854, z1: 1.645636, q1: 0.950081, r: 0.001613
q: 0.975000, z: 1.959964, z1: 1.960594, q1: 0.975037, r: 0.001471
q: 0.990000, z: 2.326348, z1: 2.326358, q1: 0.990000, r: 0.000027
q: 0.995000, z: 2.575829, z1: 2.575264, q1: 0.994992, r: -0.001635
q: 0.999500, z: 3.290527, z1: 3.288966, q1: 0.999497, r: -0.005561
q: 0.999950, z: 3.890592, z1: 3.890511, q1: 0.999950, r: -0.000335
q: 0.999995, z: 4.417173, z1: 4.420750, q1: 0.999995, r: 0.016409

0.5 がエラーになると思っていたが、特に問題はなさそう。元の分位に戻したときの相対的な差は多くの場合1％以下に抑えられている。個人的はこれで満足である。

ただし、標準正規分布表と比べたときに、一番下の段の方では、違いが出てくる。

まとめ

山内 1965

sqrt(-log(4*Q*(1-Q))*(2.0611786-5.7262204/(log(4*Q*(1-Q))+11.640595)))

ただし、Q は分位（割合・確率）。

ちなみに、mysql では、これらの整数を4 の代わりに 4.000000 としてやらないと、計算してくれないことがあるので注意

*1:分位という言葉は正しいかわからないが、ここでは分位点を調べるための割合、確率をいう

2018-01-15

scikit learn の Kfold, StratifiedKFold, ShuffleSplit の違い

背景

scikit learn の cross validation にて、テスト事例の分割方法に Kfold, StratifiedKFold, ShuffleSplit, StratifiedShuffleSplit というのがある（他にもある）。その違いがわかりにくい。

Kfold と StratifiedKFold の違い

Kfold は知っているという前提で、StratifiedKFold は、その説明にある通り、

The folds are made by preserving the percentage of samples for each class.

その分割は、サンプルのそれぞれのクラスの割合を保ったまま作られる（超意訳）。

ということらしい。100個のデータがあって、クラス１とクラス０に、それぞれ5個と95個属するとき、それぞれのクラスの割合は、5%と95％である。よって、その5%と10％を保ったまま分割されるということだ。

でもこのデータを10-Fold にする場合はどうなるのだろうか？ 10個づつになるわけだから、0.5個と 9.5個に分割しないとクラスの割を保ったままに出来ないはずだが、そのような分割はできない。だから、そもそもこのようなマイナーなクラスが小さなデータの場合、理想的にクラスの割合が等しく分割することは出来ない。マイナーなクラスのための機能のような気がするのに、だ。結果として、

The least populated class in y has only 5 members, which is too few. The minimum number of labels for any class cannot be less than n_folds=10.

といったようなメッセージを見るかもしれない。これはコード内のコメントを読むと、例外を出す代わりに trim すると言っている。コードを読み切れていないが、すでに k-fold とはよべないような状況が起きている気がする。（例えばマイナーなクラスの事例が別の分割(fold)にも重複して使われたり…）

KFold と ShuffleSplit の違い

こちらも、 KFold は知っているという前提で話をすすめる。 KFoldのとの大きな違いは ShuffleSplit は繰り返し再サンプリングする。よって、k 回行うと重複して同じ事例がでてくるかもしれない。この ShuffleSplit は事例の数を減らして（ダウンサンプリングして）学習させる際に、別のダウンサンプリングでも結果がそれほど変わらないかを検証する際に使うらしい。

だから、KFold のオプション shuffle=True と同じ結果になるわけではないことに注意。

ちなみに shuffle オプションはデフォルトで、False なので、 shuffle=True をつけないと、事例をランダムにソートしてくれない。

まとめ

クラスの割合を保ったまま分割したときは、StratifiedKFold を使う。
ただし、マイナーなクラスの事例数が少ない（特に分割数より少ない）と警告が出て、その場合は想定外の結果となるだろう。
ShuffleSplit は KFold の shuffle=True ではなく、特にデータが大きい場合のダウンサンプリングのばらつきなどを検証するために使う（複数の分割において重複するかもしれない）

なお、GridSearchCVの説明によると、推定器か教師データが二値か多クラスの場合、デフォルトで、StratifiedKFold になるそうである。もちろん、shuffle は Falseになっている。 scikit learn は初心者向けのようで実は…

参考

stackoverflow.com

https://www.kaggle.com/ogrellier/kfold-or-stratifiedkfold

背景

解決法

背景